Wer ist online?
Buchempfehlung
FreeBASIC-Chat
FreeBASIC-Nachrichten jetzt auch über Twitter erhalten. Follow us!Tutorial
Neuronale Netze - 1. Perceptron
von  chutullu | Seite 1 von 1 |
Neuronale Netze - 1. Perceptron
1.1.0. Grundlagen
Künstliche Intelligenz ist ein Sammelbegriff für verschiedenste Techniken, mit denen menschliches Denken
nachgeahmt werden soll. Dabei kristallisiert sich eine Gemeinsamkeit heraus, die Fähigkeit einer "Maschine"
zu lernen.
Unter Neuronalen Netzen versteht man die Nachahmung lebender Gehirnstrukturen, diese werden als elektrisch
verarbeitende Elemente angesehen und mittels Hard- bzw. Software nachgebildet. Somit ist unser Gehirn nichts
anderes als ein massiv parallel arbeitendes Neuronales Netzwerk.
Die Fähigkeit sich die Muster zu merken, wird in der Natur durch die verschiedenen Verbindungen (Synapsen)
zwischen den einzelnen Gehirnzellen (Neuronen), welche man sich als eine Art elektrischen Wiederstand
vorstellen kann, realisiert, der Biologe möge mir die vielleicht etwas "schwammige" Formulierung verzeihen.
1.1.1. Einteilung der Netzparadigmen
Neuronale Netze können nach verschiedenen Gesichtspunkten unterschieden werden :
- Lernart (supervised / unsupervised)
- Netzarchitektur ( Feedforward Netze / Feedback Netze / einschichtig / mehrschichtig)
- Eingabe / Ausgabe Verhältnis (Mustererkennung / Assoziierung)
- Erkennen der Muster ( bekannte und gelernte Muster erkennen / selbstorganisierende Auffindung von Musterklassen)
- Wertebereich der Ein-/Ausgangssignale (diskrete Werte / kontinuierliche Werte)
- Art der Berechnung
1.2. Perceptron
Zum Einstieg eignet sich besonders das Perceptron, dieses stellt das älteste Neuronale Netz dar.
Unter einem Perceptron ist ein Sensor mit verschiedenen Eingängen zu verstehen, der fähig ist
die Eingangswerte in zwei verschiedene Klassen zu unterscheiden. Dies wird durch eine Hard Limiterfunktion
am Ausgang ermöglicht.
Im Prinzip besteht ein Perceptron aus :
- Eingangswerten und einem Bias Wert (diskrete Werte [0,1])
- Gewichtungen (eigentliche Speicher)
- einer Summenfunktion
- Ausgang als Hard Limiter (0 oder 1)
Zum besseren Verständnis die grafische Darstellung des Perceptrons :
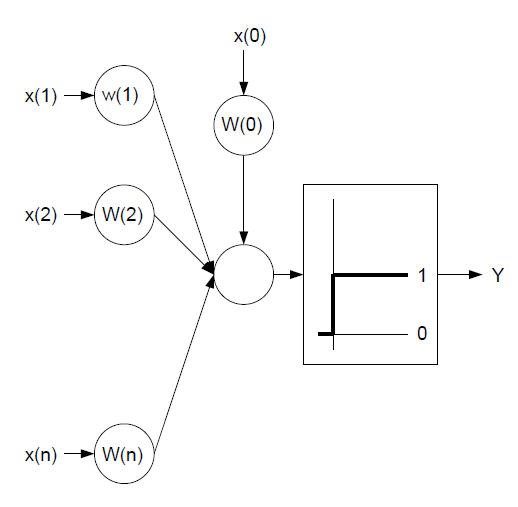
Softwaretechnisch kann dies folgendermaßen realisiert werden :
Type perceptron
AnzEingang As Short 'Anzahl der Eingänge
Eingang As Byte Ptr 'Eingänge (x - Werte)
gewAusgang As Byte 'gewünschter Ausgang
Bias As Byte 'Bias (x(0) - Wert)
Gewichte As Double Ptr 'Gewichte
Declare Function Ausgang () As Byte 'Ausgang
Declare Sub Lernen () 'lernen
End Type
Die Summenfunktion ist nichts anderes als eine einfache Schleife, welche den ersten bis zum letzten Eingangswert mit der jeweiligen Gewichtung multipliziert und gleichzeitig den Bias Wert [x(0)], welcher rein fiktiv und immer eins ist, addiert. Die anschließende "Hart Limiter" Funktion entspricht einer IF Anweisung, entweder Null oder Eins :
Function perceptron.Ausgang () As Byte
Dim a As Short
Dim sum As Double
With this
For a = 0 To AnzEingang - 1 : 'wir beginnen bei Null zu zählen
sum += (.Eingang[a] * .Gewichte[a]) + .Bias
Next a
'Hart Limiter
If sum < 0 Then Return 0
If sum >=0 Then Return 1
End With
End Function
Der Code für die Generierung des Ausganges zeigt sehr schön wie ein Neuronales Netzwerk arbeitet und es ist ersichtlich, dass der Ausgangswert von den Gewichtungen abhängt. Die Gewichtungen werden mit der sogenannten "Delta Regel" gelernt. Die "Delta Regel" zählt zu den "supervised" Lernverfahren, wobei es sich dabei sepziell um die partielle Ableitung des quadratischen Fehlers handelt. Ich enttäusche den fleißigen Mathefan und werde nicht weiter auf die Herleitung der iterativen Formel eingehen :
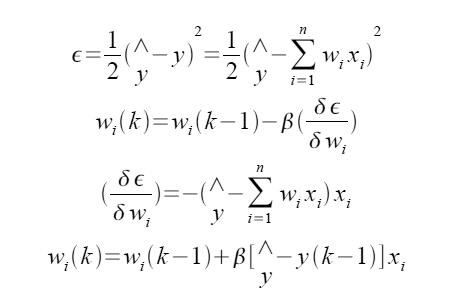
oder auf Deutsch
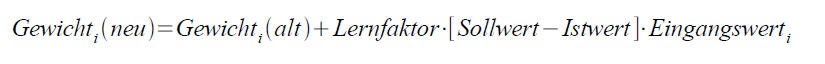
Für den Lernfaktor wird ein Wert zwischen 0..1 (meist ein Erfahrungswert) benötig. Ich nehme im allgemeinen
0.025, was einen relativen langsamen Lernprozess nach sich zieht. Bei komplizierteren Netzwerken muss einfach probiert werden, was am besten funktioniert. In FreeBasic lässt sich die Funktion wie folgt darstellen :
Sub perceptron.Lernen ()
Dim a As Short
With this
For a = 0 To AnzEingang - 1
.Gewichte[a] = .Gewichte[a] + LF * (.gewAusgang - .Ausgang) * .Eingang[a]
Next a
End With
End Sub
Hier sind wir schon am Ende des Perceptrons. Eine Zusammenfassung des Themengebietes gibt folgender kleiner Quellcode, welcher ein Perceptron - Element darstellt und dessen Einsatz als AND Funktion zeigt. Es empfiehlt sich mit dem Lernfaktor zu experimentieren, weiterhin ist es für das Verständnis ratsam, während der einzelnen Lernschritte einmal alle Gewichtungen auszugeben.
Viel Spaß beim Experimentieren.
' Perceptron - Grundlage
'
' Allgemeine Beschreibung
'
' Das Perceptron setzt sich wie fogt zusammen :
'
' Eingang : x(1) .. x(n)
' Gewichte : w(1) .. w(n)
' Summenfunktion : sum = x(1)*w(1)+w(0) + x(2)*w(2)+w(0) + ... + x(n)*w(n)+w(0)
' Hart Limiter : y = 1 wenn sum >= 0 oder y = 0 wenn sum < = 0
'
' Die Variable w(0) nimmt eine Sonderfunktion ein, sie wird "Bias" genannt und
' hat den Wert 1. Weiterhin sind die Eingangs-/Ausgangswerte so genannte diskrete
' Werte, d. h. sie können nur den Wert 0 bzw. 1 annehmen.
'
' Lernvorgang
'
' Supervised, d.h. es werden Eingangsmuster und Ausgangsmuster vorgegeben.
' Dabei wird die so genannte Delta Regel verwendet :
'
' Gewicht (k) = Gewicht (k - 1) + Lernfk. * (Sollausgang - Istausgang (k - 1)) * Eingangswert
' i (neu) i (alt) i
'
Type perceptron
bias As Byte
weights As Double Ptr
LEARN_FACTOR As Double
numWeights As Short
InValue As Byte Ptr
OutValue As Byte
Declare Constructor ()
Declare Constructor (ByVal As Short)
Declare Destructor ()
Declare Sub reset_in ()
Declare Sub reset_out ()
Declare Sub reset_weights ()
Declare Sub reset_all ()
Declare Function outp () As Byte
Declare Sub learn ()
End Type
Constructor perceptron ()
With this
.bias = 1
.numWeights = 10
.InValue = Callocate (SizeOf (Byte) * .numWeights)
.weights = Callocate (SizeOf (Byte) * .numWeights)
.LEARN_FACTOR = 0.1
End With
End Constructor
Constructor perceptron (ByVal numOfInputs As Short)
With this
.bias = 1
.numWeights = numOfInputs
.InValue = Callocate (SizeOf (Byte) * .numWeights)
.weights = Callocate (SizeOf (Byte) * .numWeights)
.LEARN_FACTOR = 0.1
End With
End Constructor
Destructor perceptron ()
With this
DeAllocate (.InValue)
DeAllocate (.weights)
End With
End Destructor
Sub perceptron.reset_in ()
With this
DeAllocate (.InValue)
.InValue = Callocate (SizeOf (Byte) * .numWeights)
End With
End Sub
Sub perceptron.reset_out ()
this.OutValue = 0
End Sub
Sub perceptron.reset_weights ()
With this
DeAllocate (.weights)
.weights = Callocate (SizeOf (Byte) * .numWeights)
End With
End Sub
Sub perceptron.reset_all ()
With this
.reset_in ()
.reset_out ()
.reset_weights ()
End With
End Sub
Function perceptron.outp () As Byte
'
'Hart Limiter Ausgang :
'
' | 1 - für y (k) >= 0
' y = <
' | 0 - für y (k) < 0
'
' _ (n)
' \ w * x + w
' y (k) = / i i 0
' - (i=1)
'
Dim a As Short
Dim sum As Double
sum = 0
With this
For a = 0 To numWeights - 1
sum += .weights[a] + .InValue[a] + .bias
Next a
If sum < 0 Then Return 0
If sum >= 0 Then Return 1
End With
End Function
Sub perceptron.learn ()
'
' Delta Regel :
' w (k) = w (k-1) + beta * (^y - y(k - 1)) * x
' i i i
'
' ^y - Sollwert
' y(k - 1) - Istwert
' beta - Lernfaktor
'
Dim a As Short
With this
For a = 0 To .numWeights - 1
.weights[a] = .weights[a] + .LEARN_FACTOR * (.OutValue - .outp) * .InValue[a]
Next a
End With
End Sub
'*****************************************************************************
' Beispiel Lösung des AND Problems mittels Perceptron
'
' Das XOR Problem lässt sich mit dem Perceptron nicht realisieren,
' da das Perceptron nur ein einfacher linearer Klassifikator ist.
'
' Aus diesem Grund wurde das Perceptron weiterentwickelt. 1960 wurde durch
' B. Widrow das Adaptive Linear Neuron (Adaline) vorgestellt. Dieses Element
' stellt den Nachfolger des Perceptrons dar.
'
Dim perc As perceptron = perceptron(2)
Dim a As Byte
Dim erg(1 To 4) As Byte
Print "AND mittels KI "
Print
Print "vor dem Lernen (untrainiertes Netzwerk) : "
Print Using ("x(1) 0 0 1 1"); ""
Print Using ("x(2) 0 1 0 1"); ""
perc.InValue[0] = 0:perc.InValue[1] = 0:erg(1) = perc.outp
perc.InValue[0] = 0:perc.InValue[1] = 1:erg(2) = perc.outp
perc.InValue[0] = 1:perc.InValue[1] = 0:erg(3) = perc.outp
perc.InValue[0] = 1:perc.InValue[1] = 1:erg(4) = perc.outp
Print Using ("y # # # #");erg(1);erg(2);erg(3);erg(4)
Print
For a = 1 To 50
perc.InValue[0] = 0
perc.InValue[1] = 0
perc.OutValue = 0
perc.learn ()
perc.InValue[0] = 1
perc.InValue[1] = 0
perc.OutValue = 0
perc.learn ()
perc.InValue[0] = 0
perc.InValue[1] = 1
perc.OutValue = 0
perc.learn ()
perc.InValue[0] = 1
perc.InValue[1] = 1
perc.OutValue = 1
perc.learn ()
Next a
Print "nach dem Lernen (trainiertes Netzwerk) : "
Print Using ("x(1) 0 0 1 1"); ""
Print Using ("x(2) 0 1 0 1"); ""
perc.InValue[0] = 0:perc.InValue[1] = 0:erg(1) = perc.outp
perc.InValue[0] = 0:perc.InValue[1] = 1:erg(2) = perc.outp
perc.InValue[0] = 1:perc.InValue[1] = 0:erg(3) = perc.outp
perc.InValue[0] = 1:perc.InValue[1] = 1:erg(4) = perc.outp
Print Using ("y # # # #");erg(1);erg(2);erg(3);erg(4)
Print
Print "ende - weiter mit taste"
Sleep
| Zusätzliche Informationen und Funktionen | |||||||
|---|---|---|---|---|---|---|---|
|
|||||||
Bearbeiten
Versionen